Section: New Results
Asymptotic and multiscale modeling in biomechanics
Detailed validations of muscle model
Participants : Matthieu Caruel, Dominique Chapelle, Alexandre Imperiale, Philippe Moireau.
Until recently we had only considered simple isotropic passive laws of Mooney-Rivlin type in our muscle model, albeit with an overall behavior already highly non-isotropic due to the fiber-oriented active component. We have now implemented and calibrated a new visco-hyperelastic passive law of exponential and orthotropic type for the hyperelastic part, in better agreement with the models and data generally found in the literature. It should be noted that most experimental data available concern the passive behavior only, indeed. In addition, we implemented a new conservative numerical scheme for the time discretization of the contractile variables. Moreover an original boundary condition of contact type has been successfully applied on several detailed cardiac geometries to represent the interactions between the epicardium, pericardium and the surrounding structures.
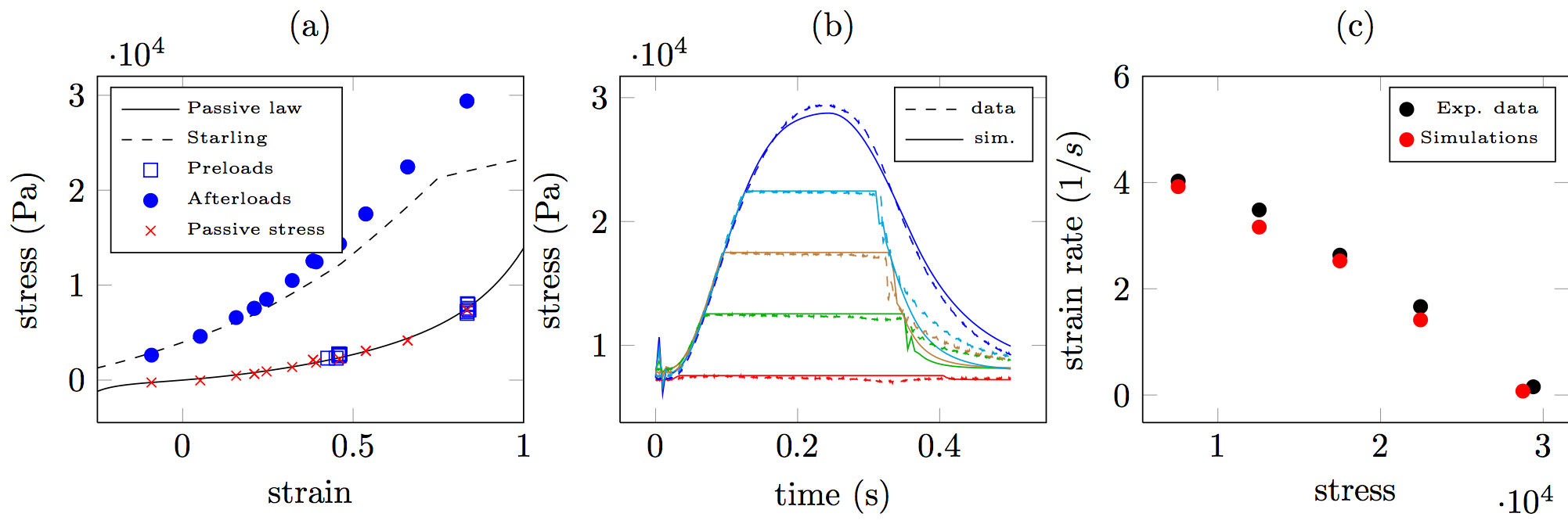
Major advances in the understanding of heart contraction cycle can be achieved by testing papillary muscle preparations in vitro. Single papillary muscles have an essentially one-dimensional structure suitable for uniaxial mechanical testing, and therefore represent the simplest setup to test the robustness of a model of heart contraction against a vast set of experimental results available in the literature. In collaboration with Y. Lecarpentier (Institut du Coeur, Pitié-Salpêtrière Hospital, Paris) and R. Chabiniok (King's College London), we have further refined and calibrated the muscle mechanical model in order to quantitatively reproduce experimental data from rat cardiomyocytes. These results include the static stress-strain constitutive relation, kinetic response to isotonic loadings, and force-velocity relation see Fig.1 .
Multi-scale mechanics of muscle contraction
Participant : Matthieu Caruel.
Muscles are an active tissue material capable of producing force. At the microscale, force is the result of complex interactions between two types of proteins, namely, actin and myosin, which work coherently in very large assemblies (
|
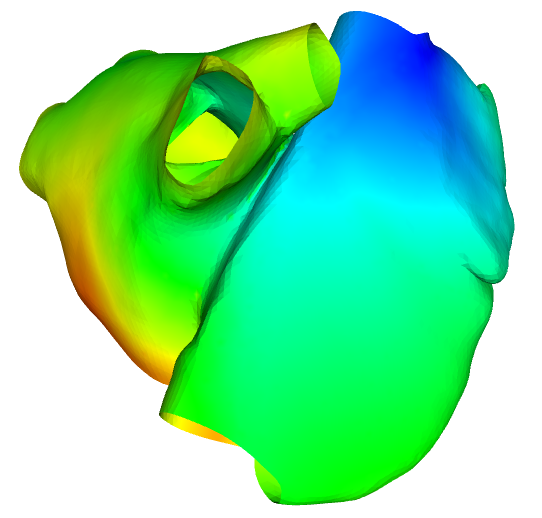
Asymptotic analysis applied to cardiac electrophysiology modeling
Participants : Dominique Chapelle, Annabelle Collin, Jean-Frédéric Gerbeau [(REO team)] .
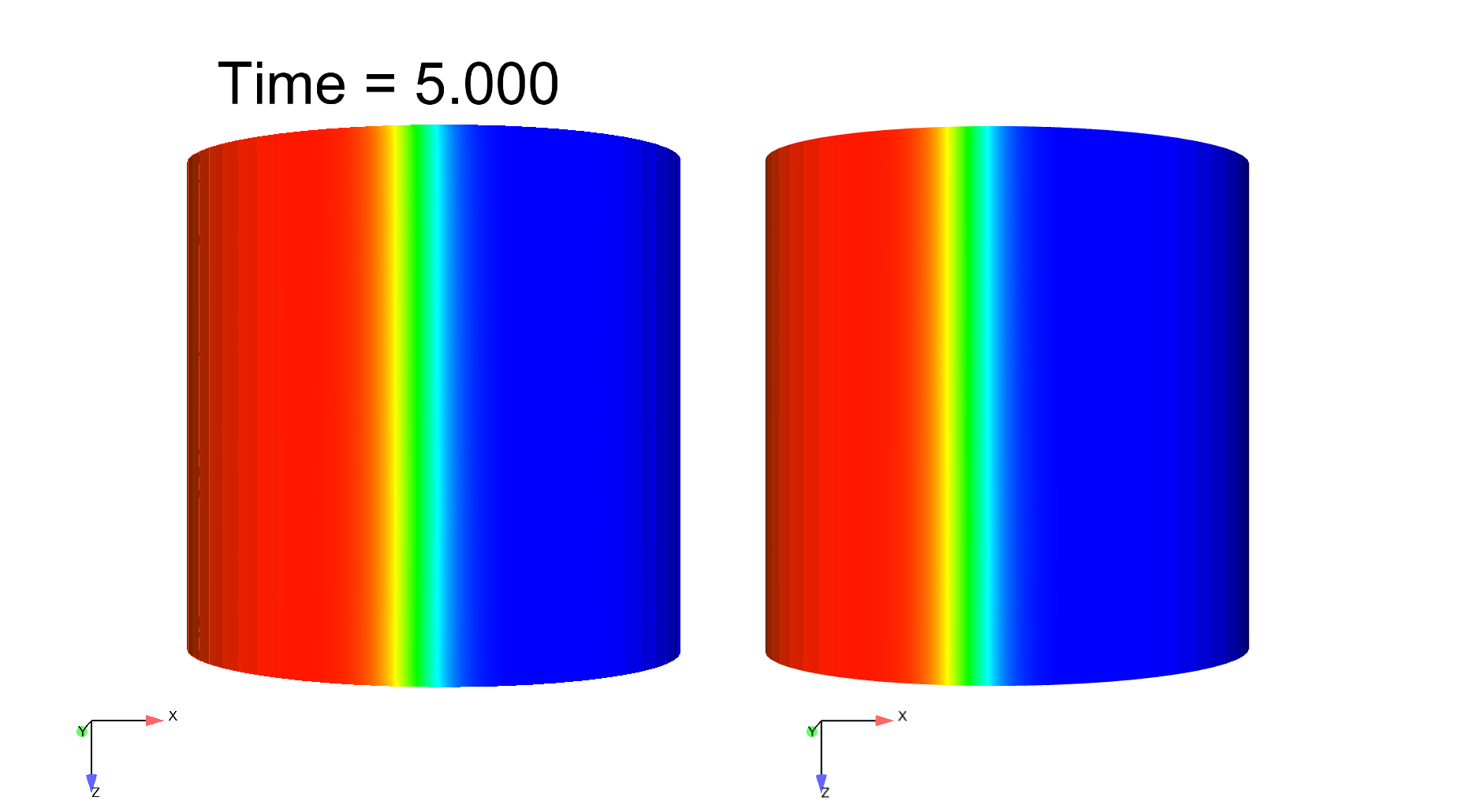
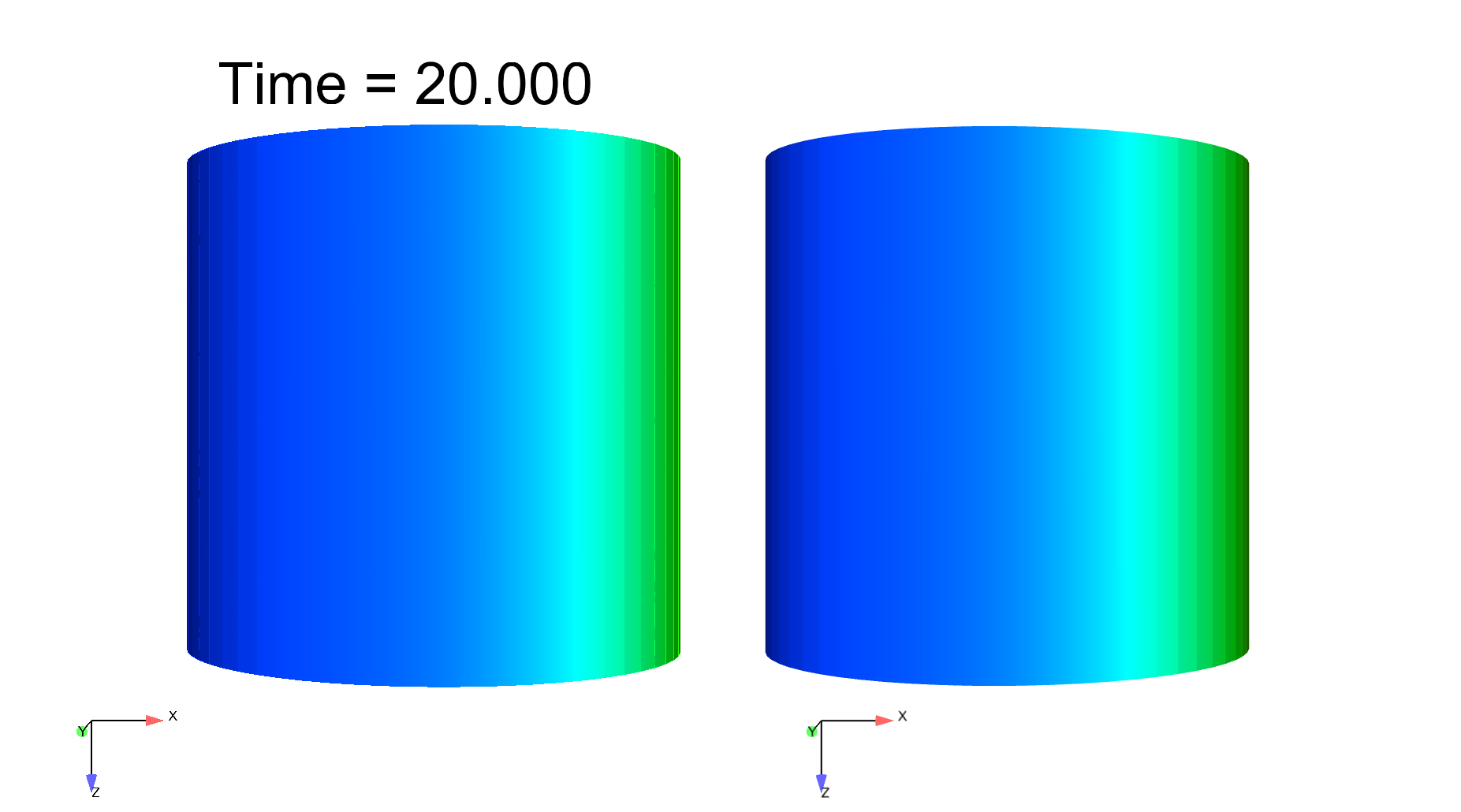
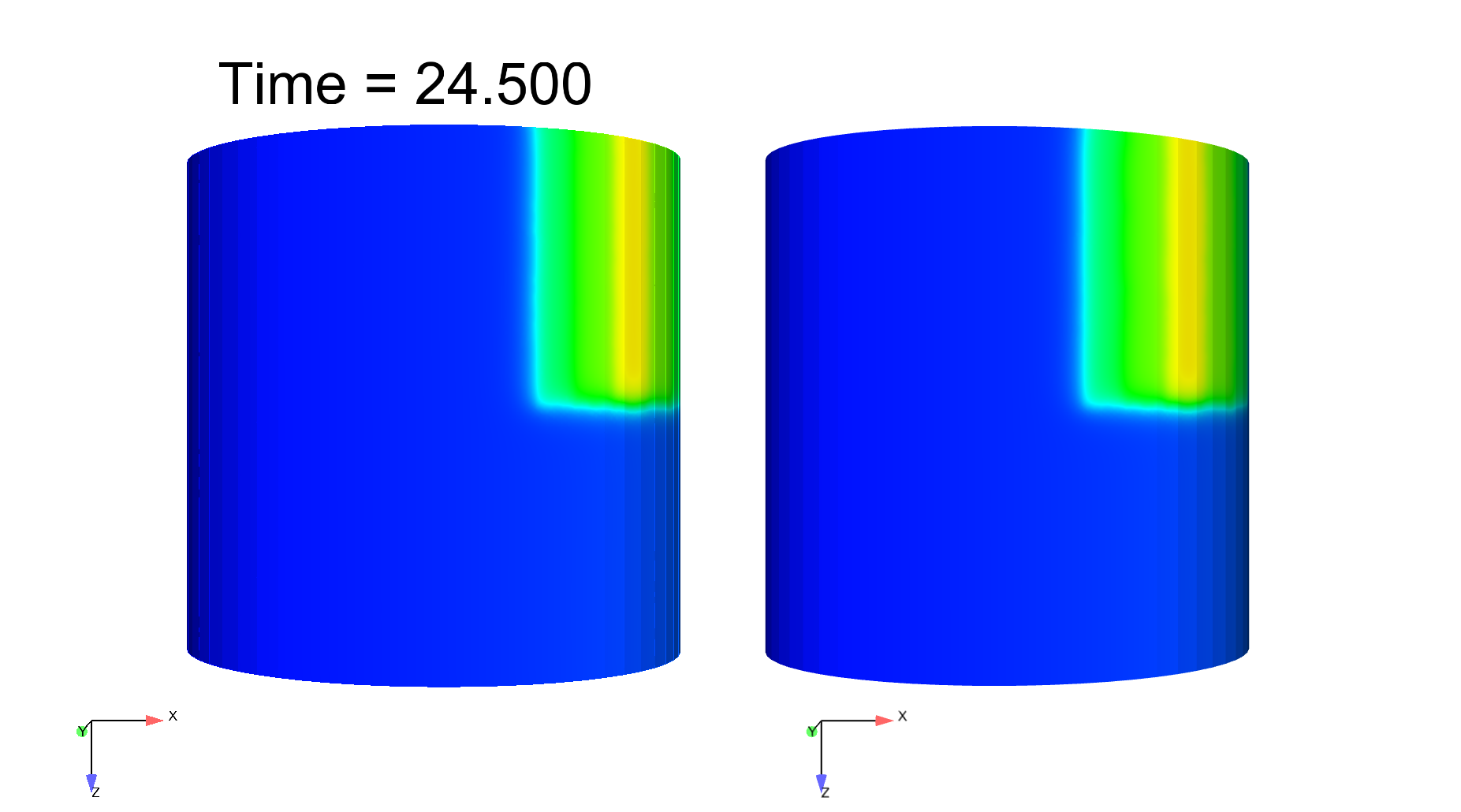
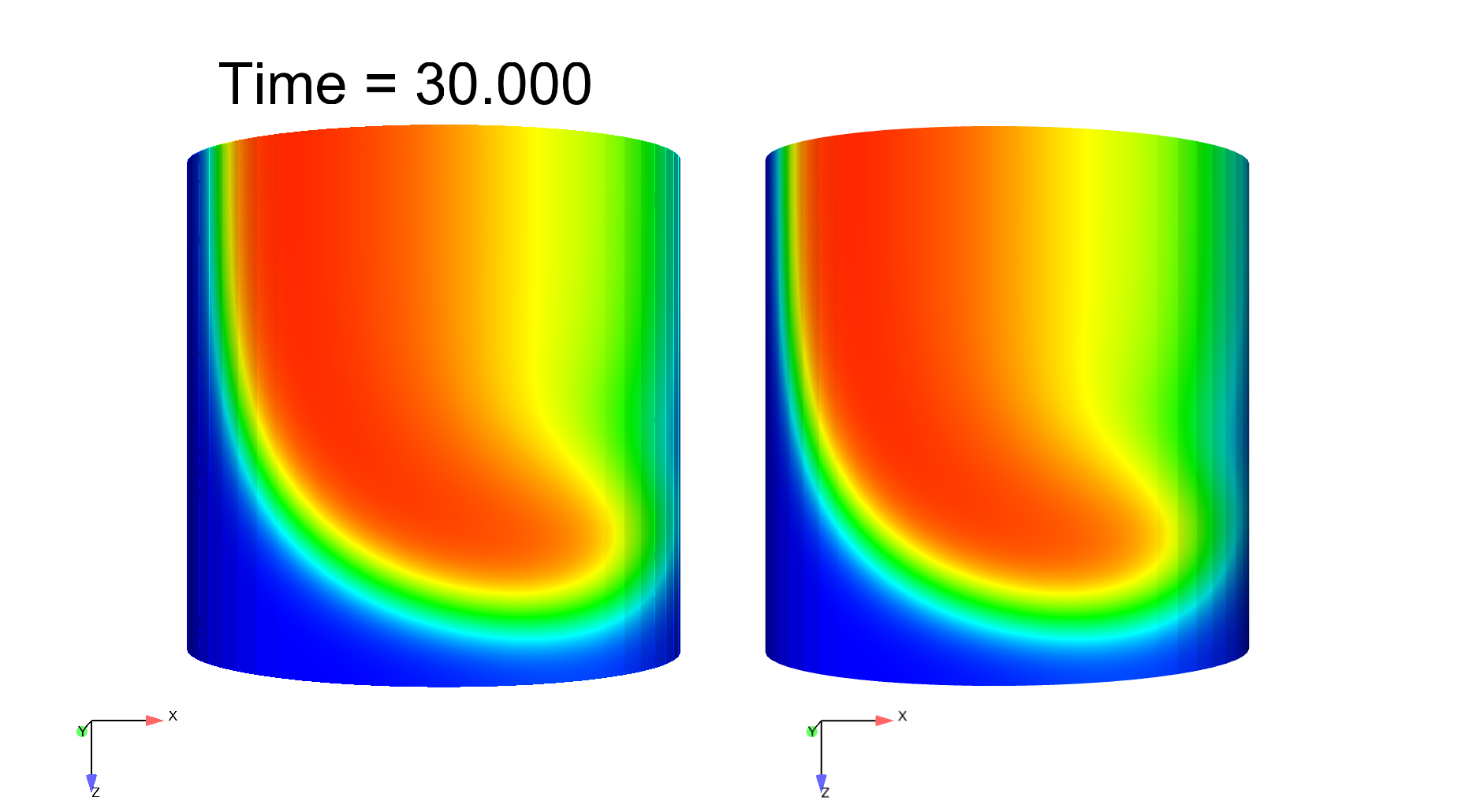
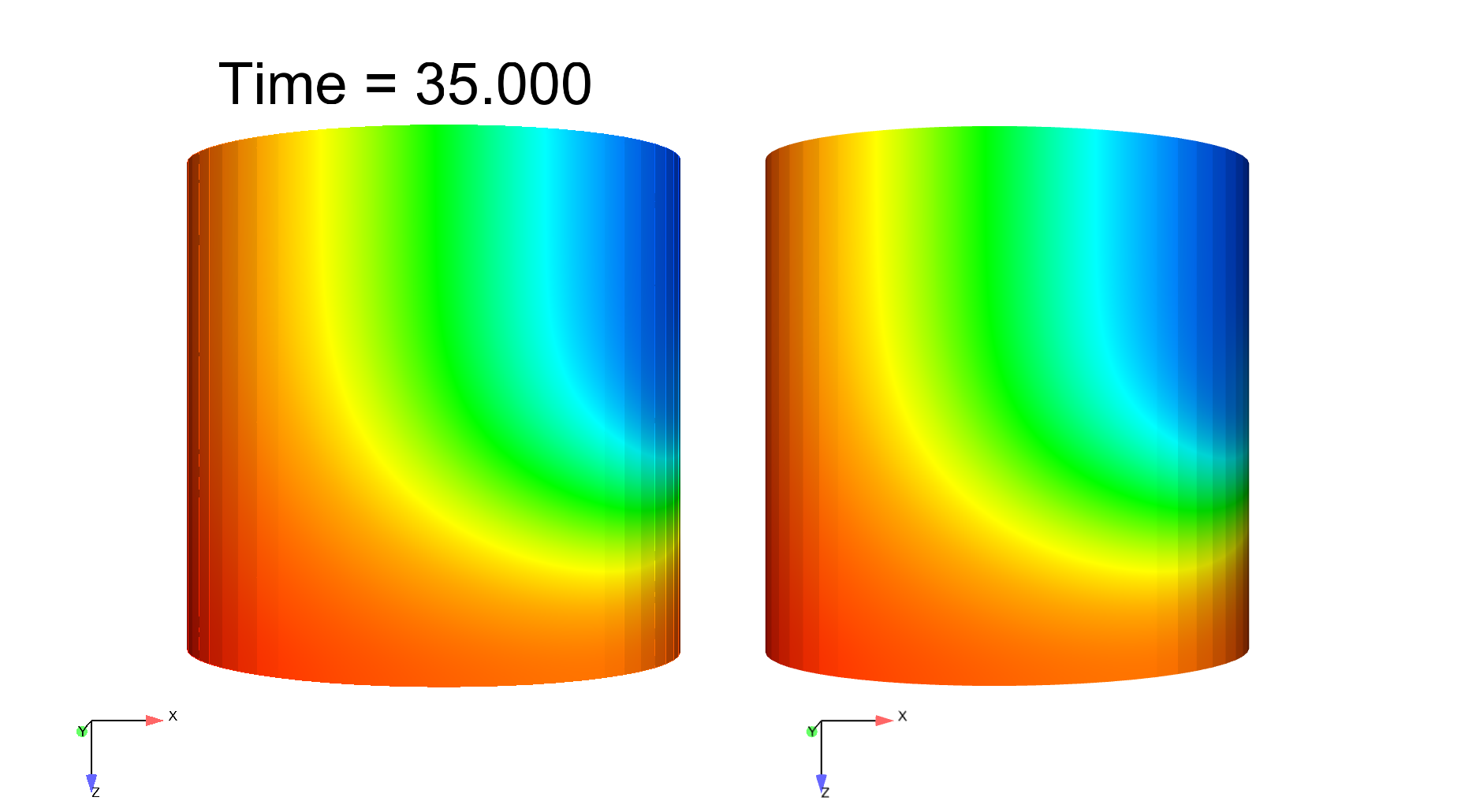
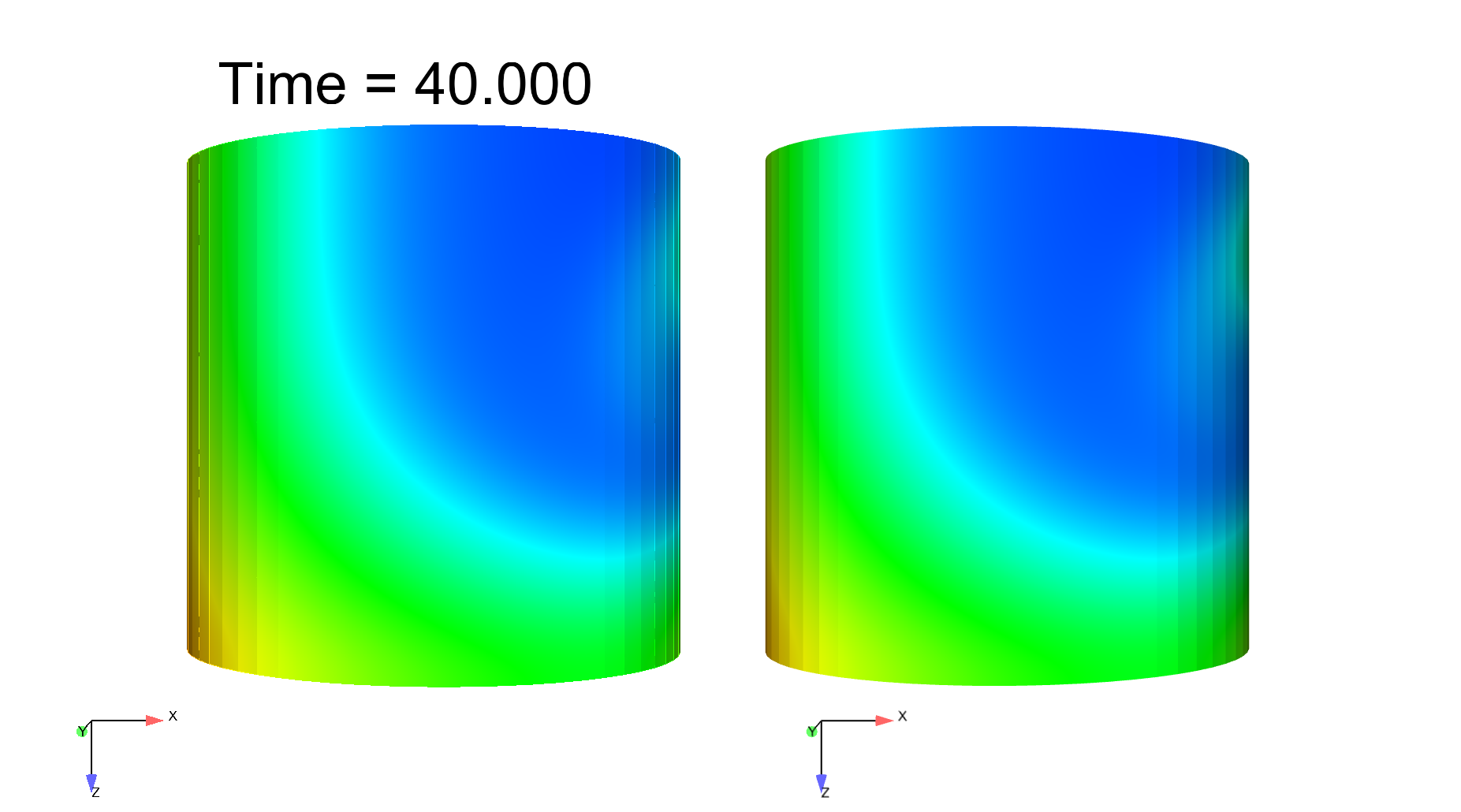
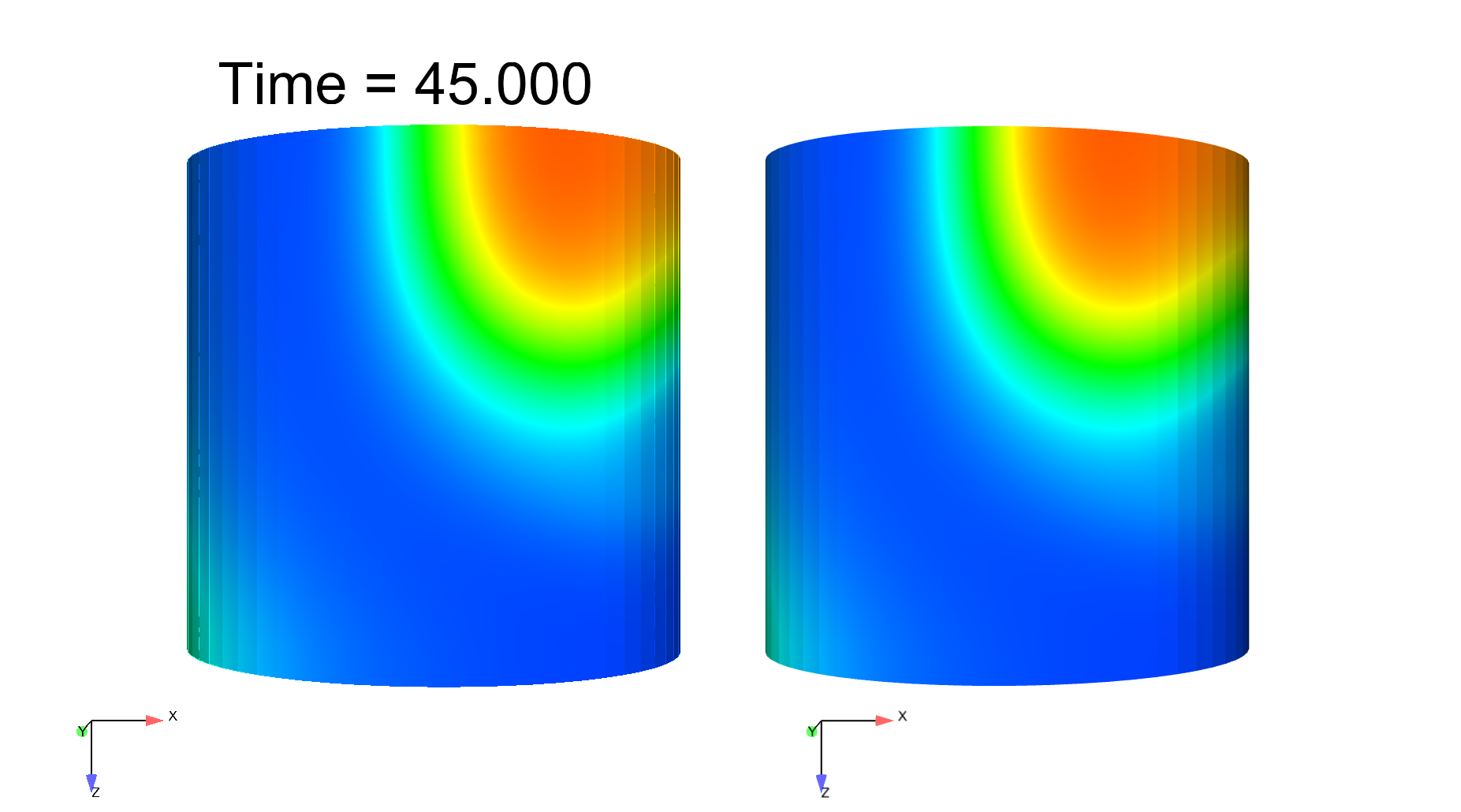
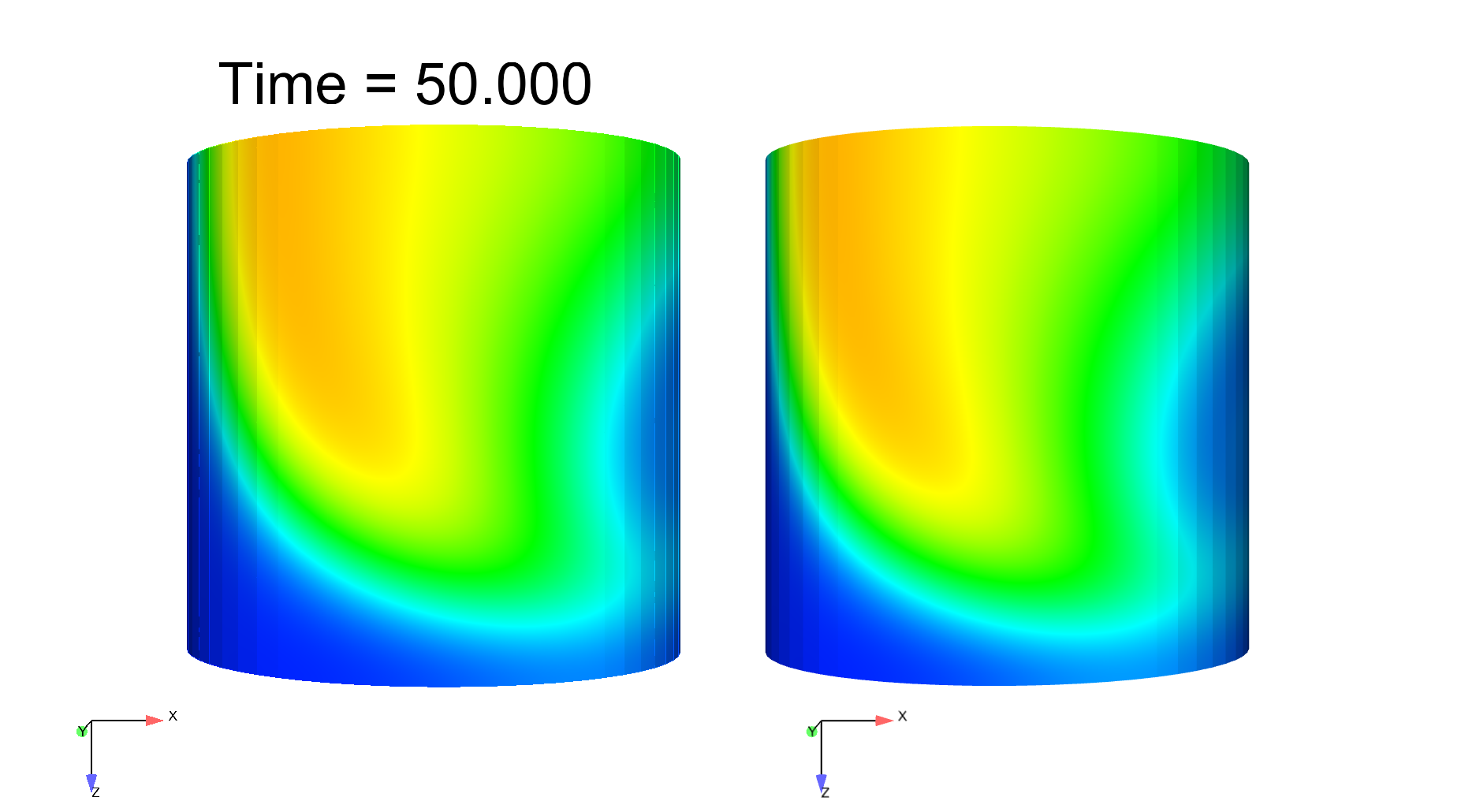
Computational electrophysiology is a very active field with tremendous potential in medical applications, albeit leads to highly intensive simulations. We here propose a surface-based electrophysiology formulation, motivated by the modeling of thin structures such as cardiac atria, which greatly reduces the size of the computational models. Moreover, our model is specifically devised to retain the key features associated with the anisotropy in the diffusion effects induced by the fiber architecture, with rapid variations across the thickness which cannot be adequately represented by naive averaging strategies. Our proposed model relies on a detailed asymptotic analysis in which we identify a limit model and establish strong convergence results. We also provide detailed numerical assessments which confirm an excellent accuracy of the surface-based model – compared with the reference 3D model – including in the representation of a complex phenomenon, namely, spiral waves, see Figure 3 . This work was submitted for publication in "M3AS: Mathematical Models and Methods in Applied Sciences".
|
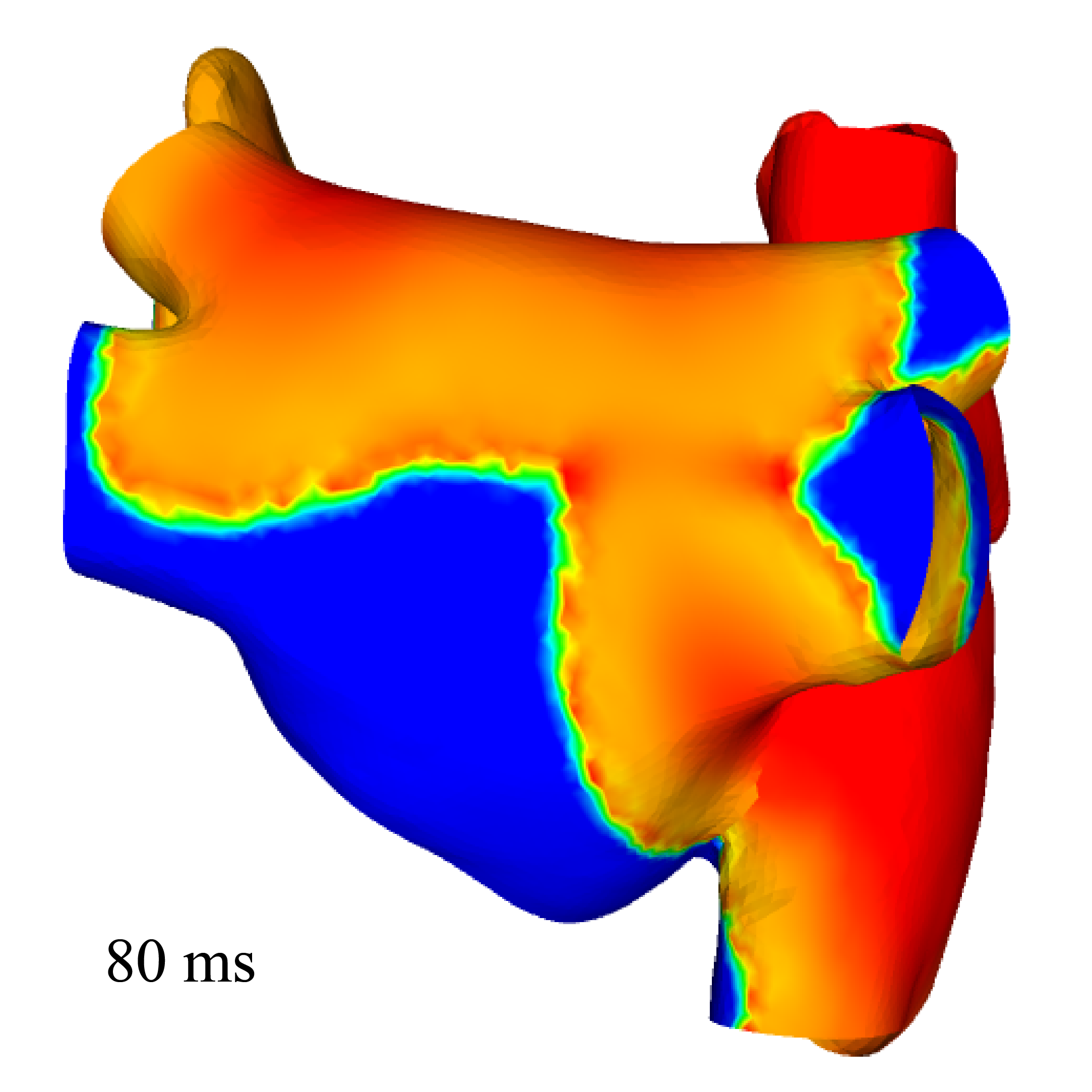
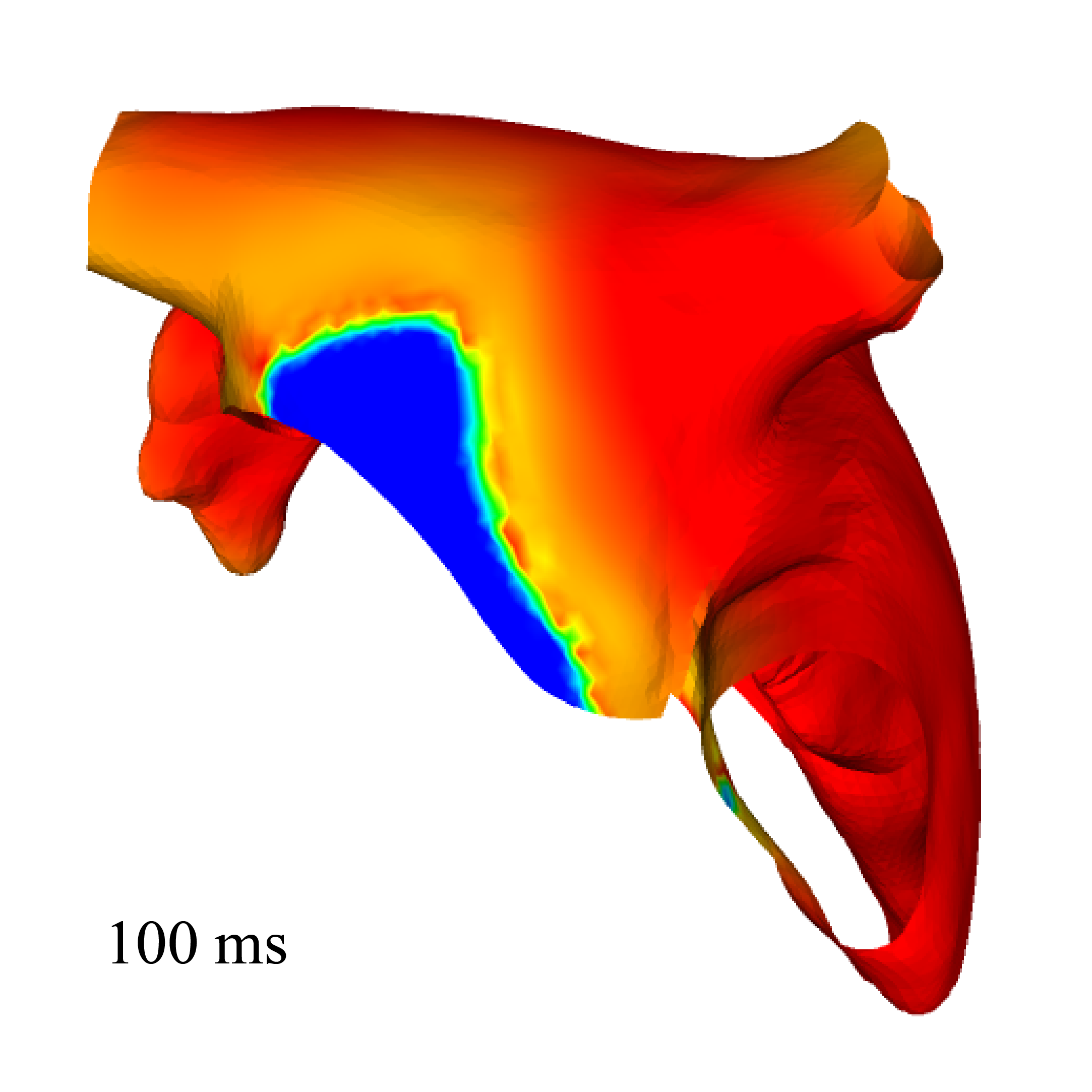
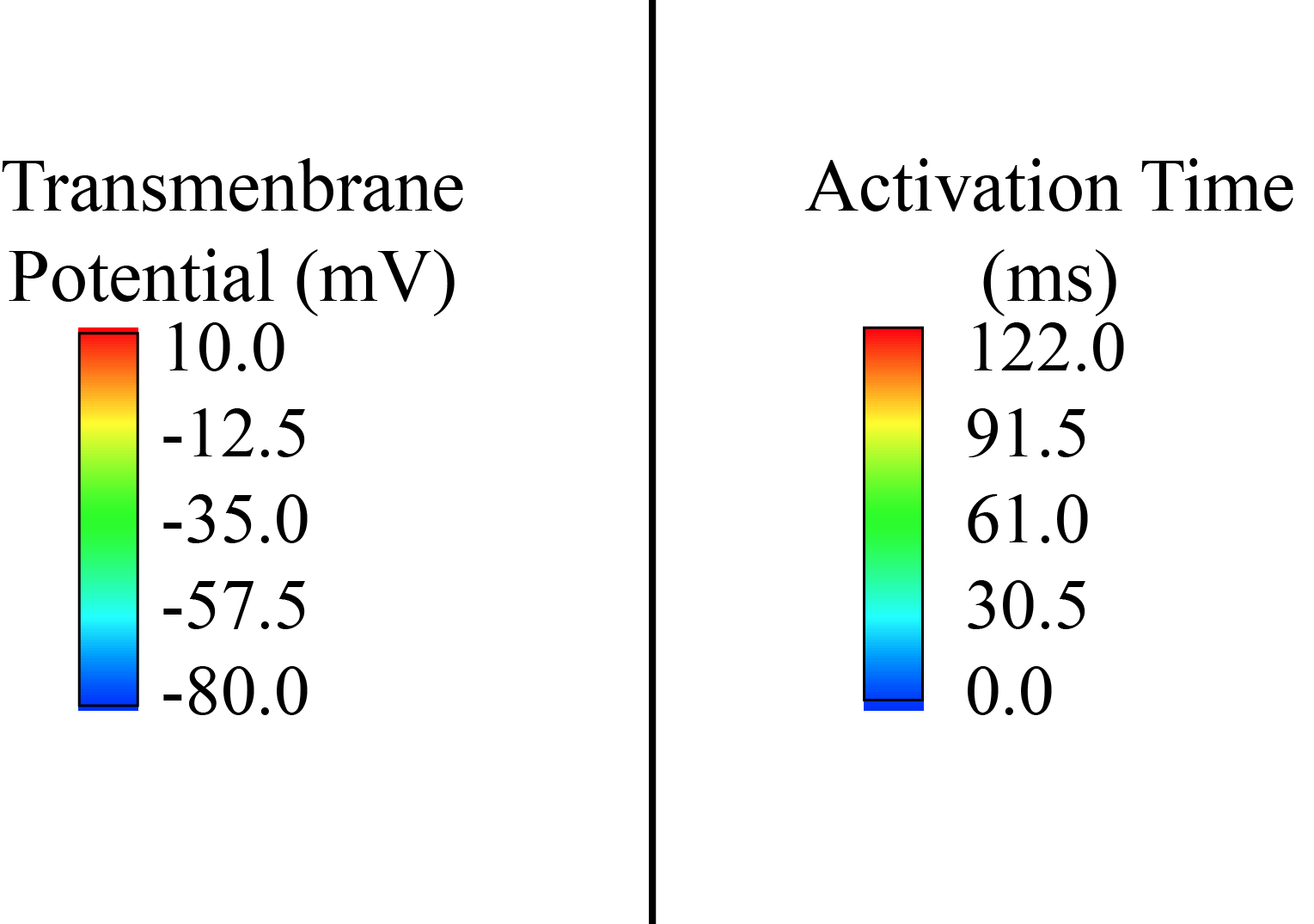
Cardiac atria electrophysiology surface-based modeling and assessment of physiological simulations
Participants : Dominique Chapelle, Annabelle Collin, Jean-Frédéric Gerbeau [(REO team)] .
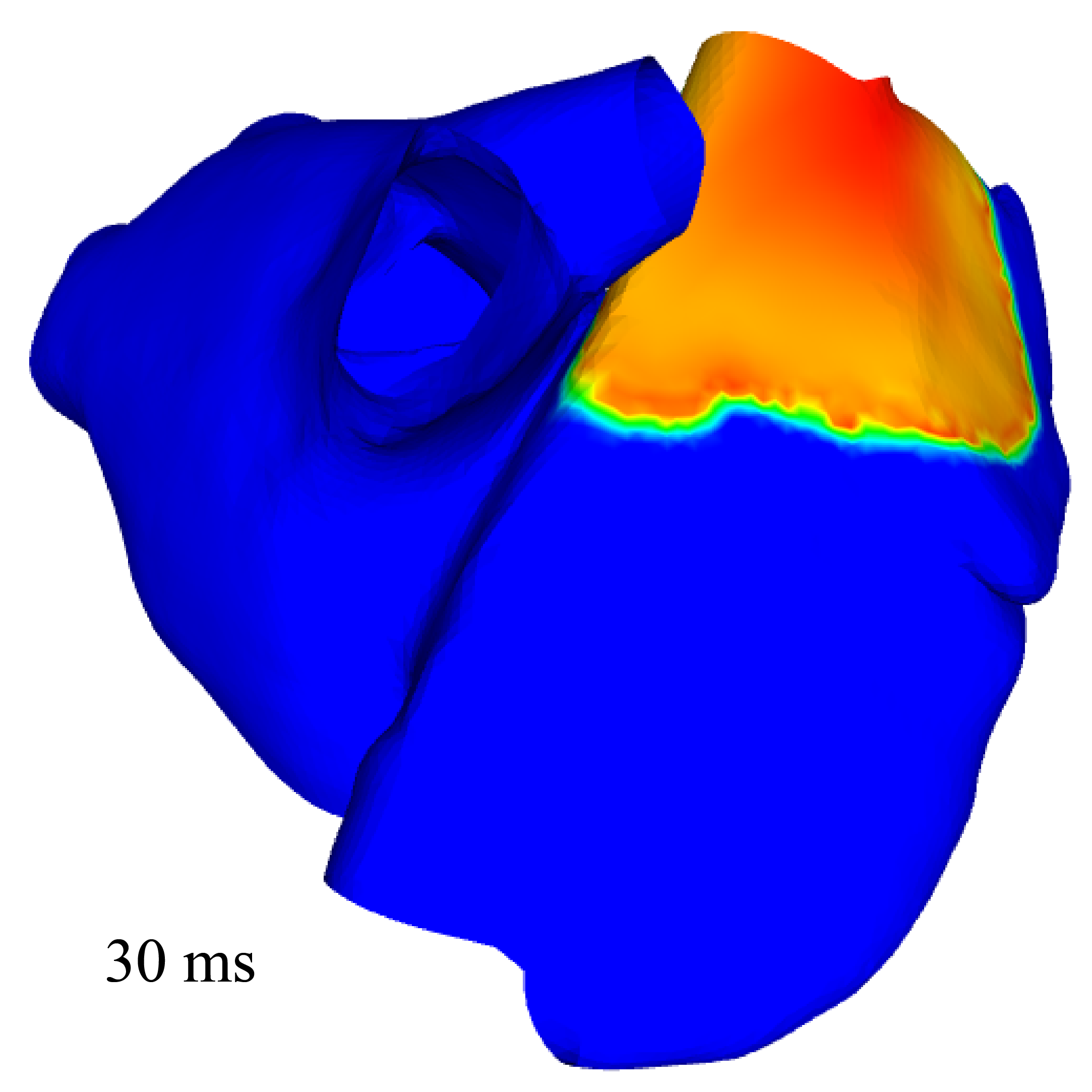
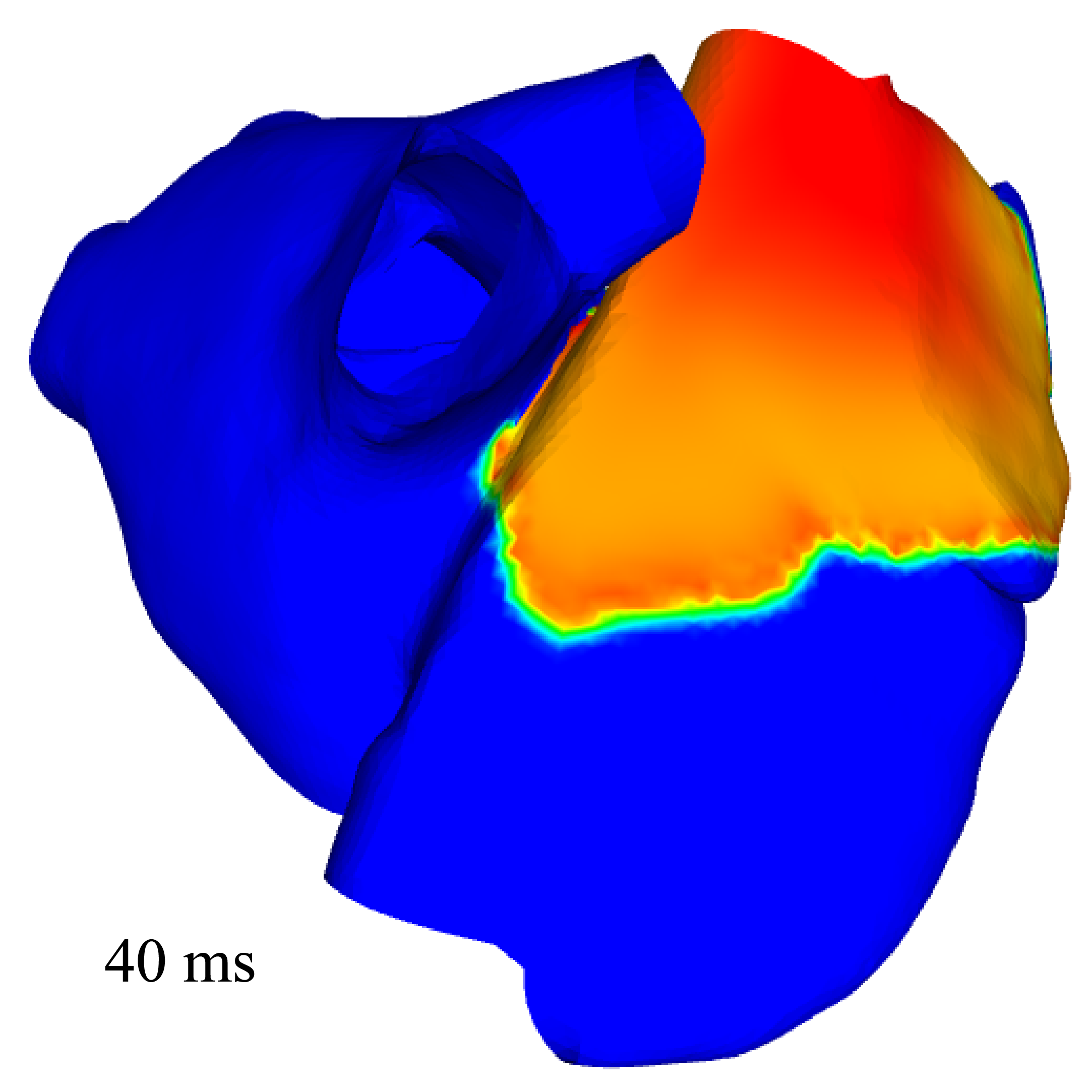
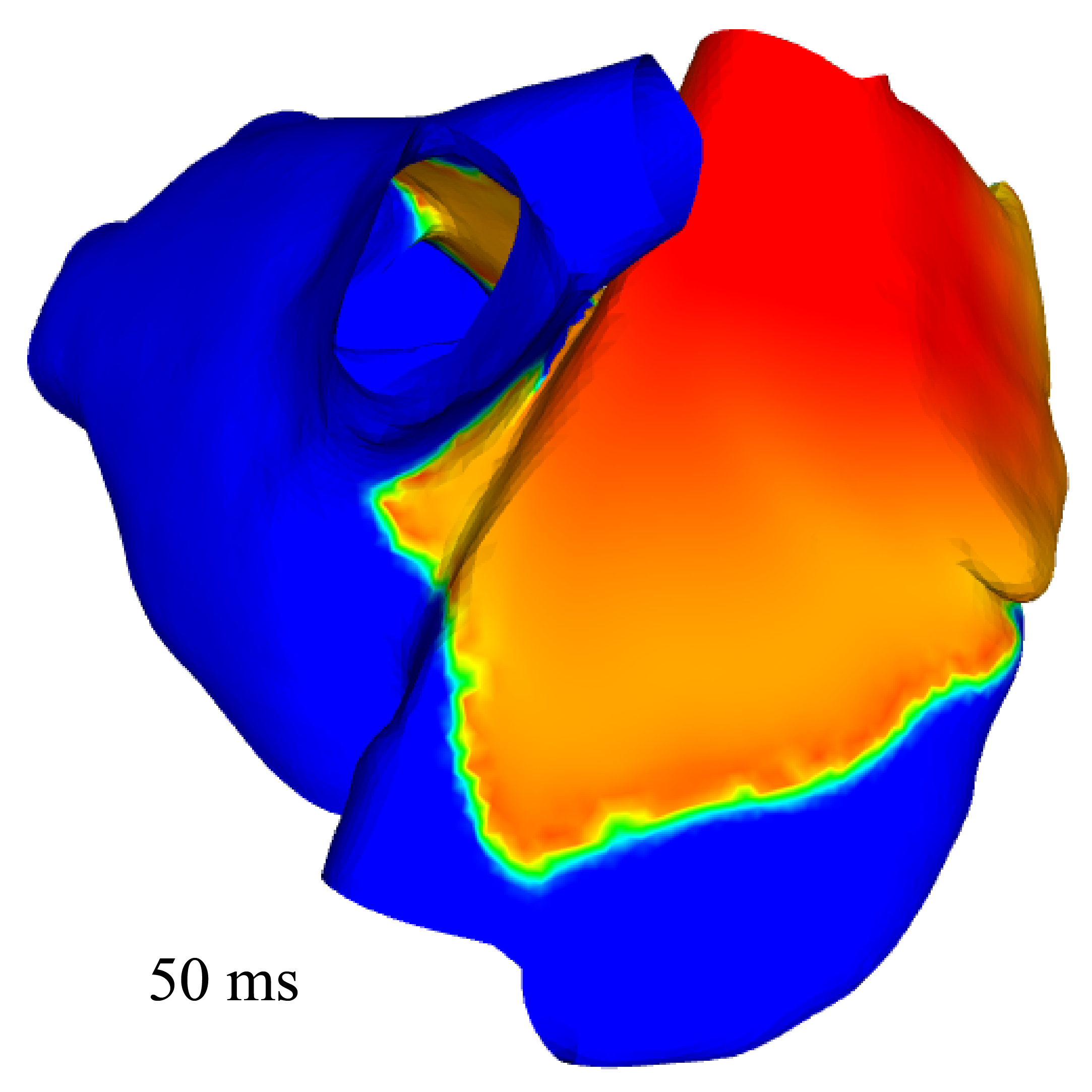
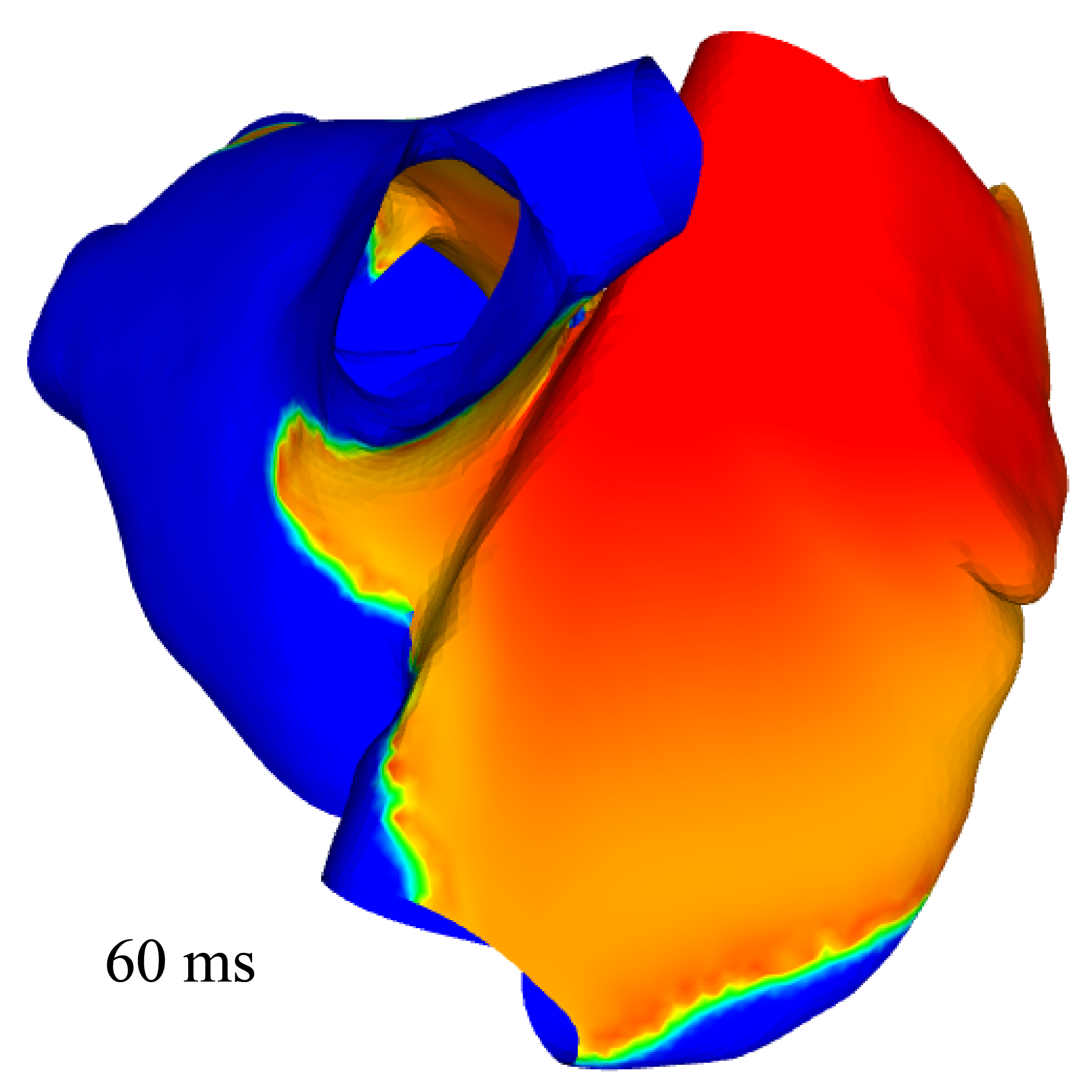
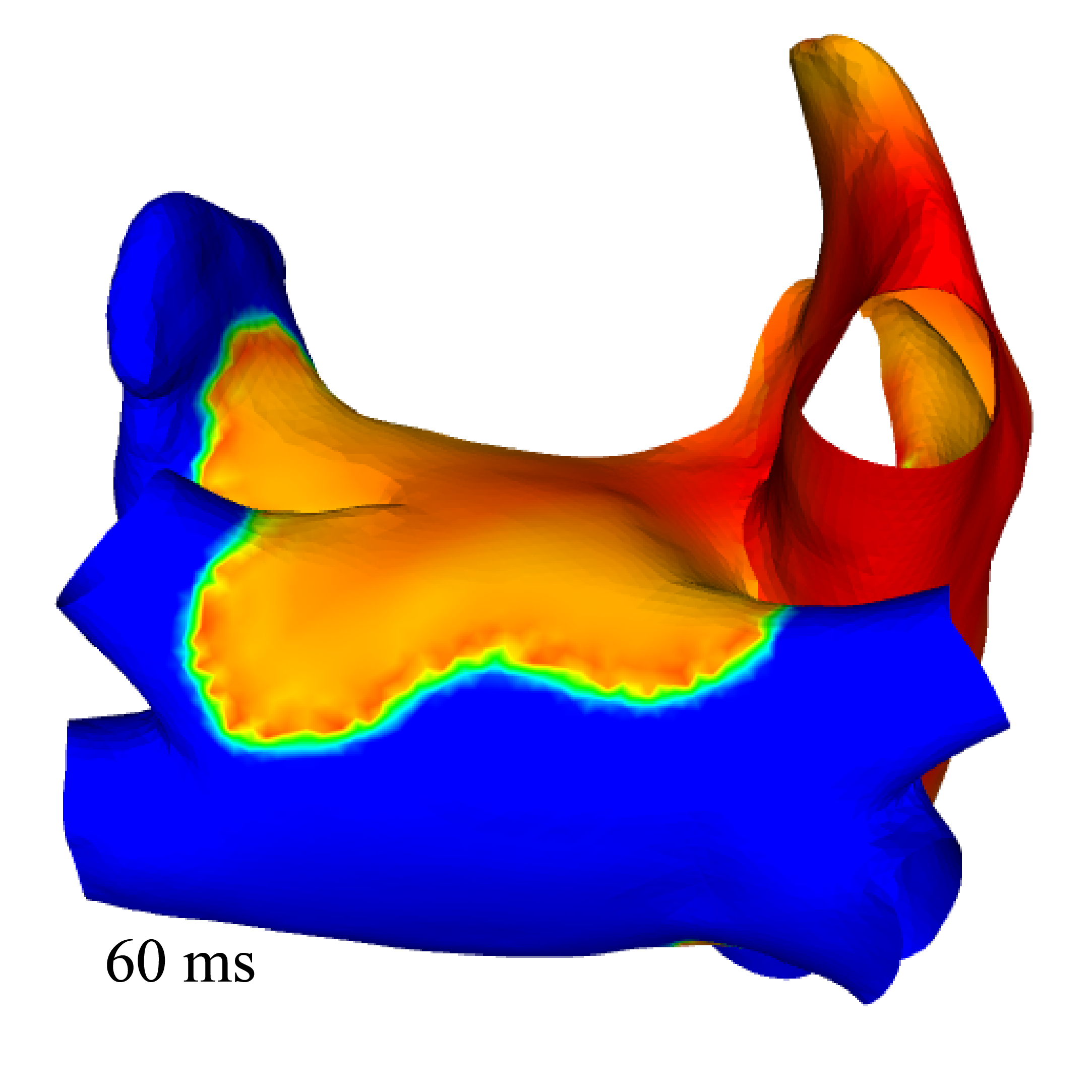
We aim at validating the 2D (namely, surface-based) electrophysiology model designed for thin cardiac structures with strongly heterogeneous anisotropy, presented in Paragraph 6.1.3 with a real model of the atria. We produced a surface mesh representing the mid-surface of the two atria. We used the bibliography to identify and prescribe the fibers directions at the endocardium and epicardium. Figure 4 displays the simulation results obtained with the surface-based model.
Strong convergence results in the asymptotic behavior of the 3D-shell model
Participants : Dominique Chapelle, Annabelle Collin.
The objective of this work is to establish the strong convergence for the asymptotic analysis of the so-called 3D-shell model presented in [2] . We apply similar methods to those used in the work on "Asymptotic analysis applied to cardiac electrophysiology modeling".